Introduzione

A* è un algoritmo di ricerca e ottimizzazione basato su grafi. Viene frequentemente impiegato nell’intelligenza artificiale perché in grado di gestire grafi ampi e indeterminati.

L’algoritmo A* può essere utilizzato per risolvere problemi come: gioco del 15, percorso minimo, Sudoku, cubo di Rubik, ecc.

In generale, A* può risolvere efficacemente i problemi che soddisfano i requisiti:

• La soluzione è determinata da cambamenti sequenziali di stato rappresentabili con grafi;
• Il nodo iniziale e il nodo finale devono essere noti. Talvolta è sufficiente conoscere solo le regole che compongono la soluzione (vedi Sudoku);
• Deve essere noto un algoritmo euristico che stima il costo del percorso tra un nodo qualsiasi e la soluzione.
• Deve essere sempre noto il costo che separa due nodi adiacenti. (Nella maggioranza dei problemi tale valore è sempre unitario).

L’euristica

L’algoritmo euristico ha il compito di stimare la distanza tra qualsiasi nodo e la soluzione. L’euristica influenza fortemente i risultati conseguiti da A*. Esso, in particolare, ne determina il tempo complessivo di esecuzione. Un algoritmo euristico molto efficace consente ad A* di trovare velocemente la soluzione. Nel caso pessimo, una funzione euristica costante, A* diviene un algoritmo di ricerca molto simile a Dijkstra.

L’euristica determina anche la qualità della soluzione finale. Con un’euristica ammissibile A* è in grado di identificare la soluzione ottima (e.g. percorso con il minor costo possibile). Un’euristica è ammissibile quando l’errore di stima non è mai in eccesso. Un esempio è la distanza in linea d’aria tra due punti su una mappa. In termini matematici una funzione euristica h è ammissibile se:

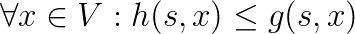
Dove V è l’insieme dei nodi, s è il nodo soluzione e la funzione g calcola la distanza esatta tra due nodi.

La funzione euristica si dice monotòna o consistente se:

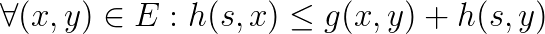
Dove E è l’insieme degli archi, s è il nodo soluzione e la funzione g calcola la distanza esatta tra due nodi.

Una funzione euristica monotona semplifica ulteriormente la struttura di A* in quanto la lista dei nodi già visitati diviene superflua. In questi casi, la sola coda a priorità è sufficiente. Una funzione euristica monotona è sempre ammissibile.

Struttura dell’algoritmo

A* rientra nella categoria degli algoritmi di ricerca best-first. Esso infatti esamina, passo dopo passo, i nodi che hanno il punteggio migliore. Esso tuttavia non è greedy in quanto il punteggio non è determinato esclusivamente dall’euristica.

A* usa le seguenti strutture dati per mantenere traccia dello stato d’esecuzione:

• Una lista di nodi già visitati;
• Una coda a priorità contentente i nodi da visitare.

Nel corso dell’esecuzione, ad ogni nodo vengono associati più valori: gScore, hScore, fScore. In termini matematici, dato il nodo corrente n, il nodo di partenza p e il nodo soluzione s, si deifiniscono i valori:

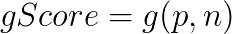
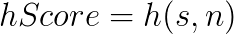
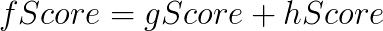
La funzione g calcola il costo effettivo del percorso che separa i nodi p (partenza) e n (attuale). La funzione h calcola una stima del costo del percorso tra i nodi s (soluzione) e n (attuale). La funzione h corrisponde alla definizione dell’algoritmo euristico enunciato in precedenza. Essa è infatti chiamata spesso funzione euristica.

La struttura dell’algoritmo A* è molto semplice. Esso, ad alto livello, può essere schematizzato in 8 passi:

1. Inserimento nella coda del nodo di partenza con priorità pari al fScore;
2. Se la coda è vuota, l’algoritmo termina: soluzione non trovata;
3. Estrazione del miglior nodo da visitare (priorità con valore più basso);
4. Se il nodo estratto ha hScore nullo, l’algoritmo termina: soluzione trovata;
5. Costruzione dei nodi figli;
6. Eliminazione dei nodi figli già visitati e subottimi;
7. Inserimento dei nodi rimanenti nella coda con priorità pari al fScore;
8. Tornare al punto 2.

In pseudo-codice:

begin function aStar(startNode)
    queue := buildPriorityQueue()
    visited := buildList()
    queue.add(startNode)
    begin while queue.isNotEmpty()
        node := queue.pop()
        begin if hScore(node) equals 0
            return node.getPath()
        end if
        children := node.getChildren()
        toInsert := buildList()
        begin for child in children
            begin if child is visited and visited.fScore > child.fScore
                toInsert.add(child)
            end if
        end for
        queue.add(<every elem in toInsert>)
    end while
    return 'No solution found'
end function

Esempio d’implementazione

Si analizza un’implementazione dell’algoritmo A* che consente di risolvere il problema del gioco del 15.

Il software è disponibile su GitHub all’indirizzo https://github.com/taueres/a-star-15-puzzle-solver

La funzione euristica utilizzata è la Distanza di Manhattan, definita nel modo seguente:

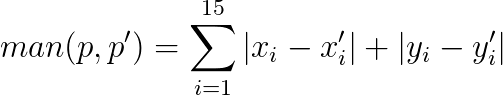
Essa calcola, per ogni casella, la quantità minima di spostamenti necessari per arrivare dalla posizione p alla posizione p’. È dimostrabile che la Distanza di Manhattan è ammissibile e monotona.

L’implementazione ha diverse componenti:

• Main.py: Stabilisce la posizione di partenza, avvia l’algoritmo e mostra la soluzione;
• Node.py: Struttura dati rappresentante ciascun nodo del grafo;
• NodeBuilder.py: Costruisce i nodi figli a partire dal nodo in ingresso;
• NodePool.py: Coda a priorità con i nodi da visitare. Esso memorizza anche i nodi già visitati con il solo scopo di non inserirli nuovamente nella coda;
• ManhattanDistance.py: Implementazione dell’euristica. Esso determina anche la posizione risolutiva del problema;
• AStar.py: Implementazione dell’algoritmo A*.

L’algoritmo mostra in output la lista dei movimenti che la casella vuota deve compiere per risolvere il problema.

Conclusioni

A* è un algoritmo semplice ma dalle grandi potenzialità. Esso getta le basi per ulteriori metodologie di ricerca più complesse come IDA* e D*. La sua principale limitazione è nell’assenza di vincoli sulla profondità di ricerca. Ciò non consente l’analisi di problemi troppo complessi come i giochi di dama e scacchi.